A continuación, profundizaremos el concepto de división con dividendos mayores que 100.
A continuación, profundizaremos el concepto de división con dividendos mayores que 100.
Por ejemplo: 1.437: 5
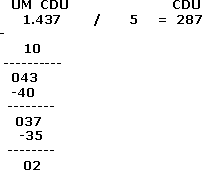
En esta división no podemos separar las U.M ., porque 5 no cabe en 1 U.M. Entonces, separamos en las C. y decimos 5 en 14 C. cabe 2 C. y sobran 4 C. Bajamos las 3 D .; ahora tenemos 43 D. y 5 en 43 D. cabe 8 D. y nos sobran 3 D. Bajamos las 7 U. y tenemos 37 U. 5 en 37 U. cabe 7 veces y nos sobran 2 U. Es una división inexacta; nos quedó 2 de residuo.
Divisiones con 0 en 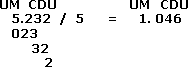 el cociente
el cociente
Algunas veces al dividir una cifra nos queda exacta, sin residuo y al bajar la siguiente, obtenemos un número menor que el divisor. Entonces, debemos colocar 0 en el cuociente y bajar la cifra que sigue.
Por ejemplo:
Separamos las U.M. 5 en 5 U.M. cabe 1 U.M. 5 · 1 = 5, resto 0. Bajamos las 2 C. 5 no cabe en 2 C.; colocamos 0 en el cuociente y bajamos las 3 D. 5 en 23 D. cabe 4 D. y sobran 3 D. Bajamos las 2 U . 5 en 32 U . cabe 6 y sobran 2.
Con calculadora
Este instrumento tan útil para simplificar los cálculos, nos trae algunas complicaciones con la división. Esto sucede porque el visor no nos muestra el resto o residuo. Si la división es exacta, no hay problema. Pero, cuando es inexacta, el cuociente aparece con un punto o una coma entre las cifras.
Por ejemplo: si digitamos 389: 7, en el visor obtenemos como cuociente 55.57142… Este cuociente es un número decimal que tú estudiarás en cursos superiores. Por ahora, toma como resultado las cifras que están antes del punto o coma, es decir, 55 en este caso.
Aproximemos
Al igual que en las operaciones anteriores, en las divisiones también se pueden hacer estimaciones de sus resultados, si realizamos aproximaciones de sus dividendos.
Veámoslo con un ejemplo. Si queremos dividir 496: 8, podríamos aproximar los 496 a 480, porque sabemos que 8 en 48 cabe 6, y en 480, 60 (agregamos el 0). También, podríamos aproximarlo a 560, porque cabría 70 veces. O sea, 8 · 7 = 56 y 8 · 70 = 560
Entonces, nuestro cuociente exacto estará entre 60 y 70.