Z es un conjunto ordenado. Esto quiere decir que hay números enteros mayores o menores que otros.
Z es un conjunto ordenado. Esto quiere decir que hay números enteros mayores o menores que otros.
Un número entero es menor que otro, si está colocado a la izquierda de él en la recta numérica; y es mayor, cuando está a su derecha.
Analicemos los siguientes ejemplos:
– Ordenaremos de menor a mayor +7, -6, +4 y -2 en la recta numérica, a partir del 0. Así, tenemos que:
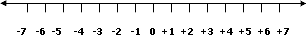
El número menor es -6, porque es el que está más a la izquierda; luego viene el -2, el 4 y el 7. En símbolos queda:
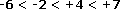
– En el siguiente ejemplo, ordenaremos de mayor a menor -1, +2, +5, 0 y -3. Tenemos:
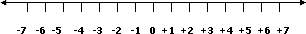
El número mayor es +5 y el menor es -3. Nos queda:
+5>+2< 0 <-1 <-3
Utiles conclusiones
Analizando los ejemplos anteriores, podemos sacar algunas conclusiones muy importantes. Estas nos servirán para ordenar números enteros sin dibujar la recta numérica:
– Todo número entero positivo es mayor que 0
– Todo número entero positivo es mayor que cualquier número entero negativo.
– Todo número entero negativo es menor que 0.
– Todo número entero negativo es menor que cualquier entero positivo.
Si expresamos estas conclusiones en símbolos, tenemos:

Nos queda determinar una fórmula para encontrar orden solo entre enteros positivos o solo entre enteros negativos. Aplicaremos el concepto de valor absoluto.
– Entre enteros positivos, es mayor el que tiene un valor absoluto mayor. Por ejemplo, si ordenamos +40, +9, +300 de mayor a menor, tenemos que: el mayor valor absoluto lo tiene 300, luego sigue 40 y finalmente 9. Entonces decimos:
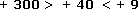
Mientras más lejos de 0 esté un número entero positivo, su valor es mayor, porque está más a la derecha.
– En los enteros negativos sucede lo contrario: mientras más lejos de 0, su valor es menor, porque está más a la izquierda en la recta numérica.
Esta conclusión nos permite determinar que en los enteros negativos, es mayor el que tiene menos valor absoluto.
Por ejemplo, ordenaremos de menor a mayor -40, -9, -300. El menor es-300, porque tiene el valor absoluto mayor, le sigue -40 y luego -9.
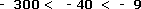
Antecesor y sucesor
Otra característica que presenta un conjunto numérico ordenado es que cada número tiene antecesor y sucesor.
Para cualquier número, es antecesor el que se ubica inmediatamente a la izquierda de él y es sucesor, el que está inmediatamente a su derecha. Observa:
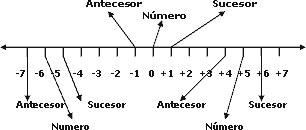
En los números naturales, el 1 no tenía antecesor; y en los cardinales, el 0 no presentaba antecesor.
En cambio, en los números enteros, todo número tiene antecesor y sucesor.