Apliquemos el teorema de Pitágoras
El gran matemático griego Pitágoras descubrió una situación muy especial que se produce en el triángulo rectángulo y que se relaciona con sus lados.
Su teorema dice: «El cuadrado construido sobre la hipotenusa de un triángulo rectángulo, equivale a la suma de los cuadrados construidos sobre sus catetos»
Demostraremos este teorema a través de un dibujo.
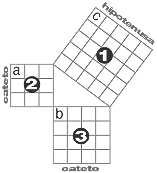
Hemos construido un cuadrado sobre cada lado del triángulo rectángulo. Pitágoras dice que el cuadrado 1 tiene su área igual a la suma de los cuadrados 2 y 3.
De acuerdo al cuadriculado, el cuadrado 1 tiene un área de 25 cuadros. Al sumar los 9 cuadros del cuadrado 2 y los 16 cuadros del 3 obtenemos 25. Entonces, se cumple:
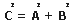
Este teorema nos sirve para calcular la medida desconocida de un lado de un triángulo rectángulo, puede ser un cateto o su hipotenusa.
Por ejemplo: si la hipotenusa mide 5 cm y uno de sus catetos es 4 cm, ¿cuánto mide el otro cateto?
Aplicamos la fórmula.
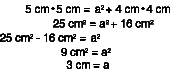
Áreas achuradas
Son una forma de aplicación del cálculo de áreas de diferentes figuras que están relacionadas entre sí. Para distinguir la parte que se debe calcular como resultado final se procede a achurarla, es decir, se pinta o raya imitando texturas.
Algunas veces, la parte achurada está formada por la unión de áreas de figuras, por lo tanto, hay que descomponerla, luego hacer el cálculo de cada parte, y finalmente, sumarlas para encontrar el área total.
Veamos el siguiente ejemplo:
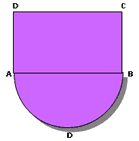
Esta figura se descompone en medio círculo y un rectángulo. Primero, tendremos que calcular el área del círculo; luego, dividirla por 2. Buscaremos, también el área del rectángulo y después sumaremos ambos resultados para obtener el área total.
– Hay ejercicios, que tienen unas figuras dentro de otras y la parte achurada se relaciona con un sector formado por la intersección de ellas. En estos casos, la solución se encuentra buscando la diferencia entre las figuras que forman la intersección. Por ejemplo:
Nuestra figura está formada por un cuadrado con un círculo en su interior. La parte achurada corresponde a la diferencia entre el área del cuadrado y la del círculo.