En el interior del polígono
Si observamos la región interior de los polígonos, podremos establecer otra clasificación.
De acuerdo a la distribución de su región interior, los polígonos se definirán como simples y no simples.
Determinaremos esta clasificación dibujando dos polígonos. Debemos tener en cuenta que los puntos se unen en el orden en el cual van sus letras. Estos son los puntos del plano:
 | I I I I I I I I I |  |
Los uniremos siguiendo su orden.
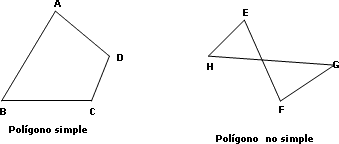
Un polígono simple presenta una sola región interior.
Los polígonos no simples tienen más de una región interior.
– Según la forma de su región interior clasificaremos los polígonos en cóncavos y convexos. Los polígonos cóncavos tienen su región interior de tal forma, que una recta puede cortar a la frontera en más de 2 puntos.
Se reconocen fácilmente, porque tienen alguno de sus ángulos interiores que mide más de 180°.
– Si unimos 2 puntos de su región interior, no siempre quedará el trazo dentro del polígono.
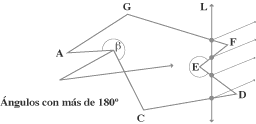 | La recta cortó a la frontera en cuatro puntos |
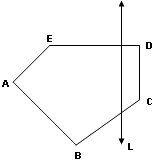
Los polígonos convexos presentan su región interior con ángulos interiores que miden menos de 180° y una recta corta a su frontera en sólo 2 puntos . Además, si unimos 2 puntos de su región interior, el trazo quedará siempre totalmente contenido en su región interior.
Las diagonales
Se llama diagonal de un polígono al trazo que une 2 vértices no consecutivos. En un triángulo no podemos dibujar diagonales, porque sus vértices son consecutivos. En un cuadrilátero, es posible dibujar dos. Para determinar cuántas diagonales se pueden trazar en un polígono, observaremos las diagonales que salen de un vértice.
En un hexágono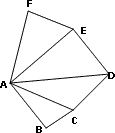 Desde el vértice A se pueden trazar 3 diagonales | En un pentágono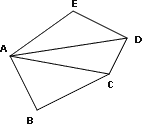 Desde A trazaremos 2 diagonales. |
Podrás observar que en el polígono de 6 lados obtuvimos 3 diagonales, desde un vértice; y en el polígono de 5 lados, sólo 2. Si te fijas, 3 menos que el número de sus lados (n – 3).
¿Cómo saber cuántas diagonales son en total?
Podríamos dibujarlas todas, pero es más fácil mediante una fórmula matemática que nos dice:
«El número de diagonales de un polígono, es equivalente a la mitad del producto entre el número de lados y el número de diagonales que se trazan desde un vértice».
Vimos que desde un vértice las diagonales equivalen a número de lados – 3. Entonces, en símbolos, tendríamos que el número de diagonales es:
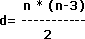
d = diagonales
n = número de lados
Un ejercicio
Revisemos cuántas diagonales tiene un dodecágono aplicando la fórmula.
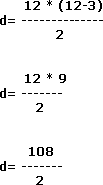
d = 54