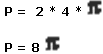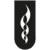En los polígonos y la circunferencia podemos realizar mediciones y cálculos. Uno de los más importantes es el cálculo del perímetro.
En los polígonos y la circunferencia podemos realizar mediciones y cálculos. Uno de los más importantes es el cálculo del perímetro.
Unidades de medida de longitud
Para medir perímetros es necesario conocer estas unidades. Las medidas de longitud miden una dimensión: el largo. La unidad base de ella es el metro (m.) El metro tiene múltiplos, es decir unidades de medida mayores que él, 10, 100 ó 1.000 veces más, y que utilizan los prefijos griegos : deca -, hecto – y kilo -, respectivamente.
Los múltiplos del metro son:
Kilómetro Hectómetro Decámetro
También existen submúltiplos del metro que equivalen a 10, 100 ó 1.000 veces menos que él. Se identifican anteponiendo el prefijo griego deci -, centi- y mili- , respectivamente. Ellos son:
Decímetro Centímetro Milímetro
Las siguientes son las unidades de medida con su equivalencia en metros:
| Unidad | Símbolo | Medida en metros |
| Kilómetro | km. | 1.000 m. |
| Hectómetro | hm. | 100 m. |
| Decámetro | dám. | 10 m. |
| Metro | m. | 1 m. |
| Decímetro | dm. | 0,1 m. |
| Centímetro | cm. | 0,01 m. |
| Milímetro | mm. | 0,001 m. |
Equivalencias
El cuadro anterior nos demuestra que las medidas de longitud tienen base 10 , igual que nuestro sistema numérico. Para establecer equivalencias , multiplicamos por 10, 100 o cualquier otra potencia de 10, según las columnas, si vamos desde una unidad mayor a una menor (de izquierda a derecha).
Aplicamos división de potencias de 10, si de una unidad menor buscamos una equivalencia con una mayor (de derecha a izquierda).
Por ejemplo:
Necesitamos saber cuántos dám. hay en 36 km. Los dám. están 2 columnas a la derecha de km., entonces, multiplicamos por 100 y nos queda:
36 km. = 3.600 dám.
Ahora, queremos saber cuántos hm. hay en 4.208,9 cm. De cm. a hm. hay 4 columnas hacia la izquierda, por lo tanto, dividiremos por 10.000. Así, tenemos:
4.208,9 cm. = 0,42089 hm.
Otra forma de establecer equivalencias entre unidades de medida de longitud, es utilizar la siguiente tabla, que aplica la operación vista anteriormente.
Dividimos Multiplicamos
<———– ————>
km. hm. dám. m. dm. cm.
Si necesitamos convertir 135,84 dám. en cm., escribiremos el numeral en nuestra tabla de la siguiente manera: Los enteros se escriben desde la unidad dada, dám., hacia la izquierda (1 cifra en cada casillero) y los decimales hacia la derecha. Corremos la coma hasta la columna pedida. Si nos faltan cifras, completamos con ceros.
km. hm. dám. m. dm. cm. mm
1 3 5 8 4 0
Como las unidades de medida son distintas, las igualaremos a cm. Entonces, 0,07 m. = 7 cm.
El perímetro del triángulo es:
12 cm. + 9 cm. + 7 cm. = 28 cm.
El perímetro de una circunferencia, es decir su longitud, se relaciona con las veces que cabe el diámetro en ella. En toda circunferencia ese cuociente es constante y corresponde aproximadamente a 3,1416… veces en la longitud de la circunferencia. A esta constante, que es un número irracional, se le designa la letra griega p.
Como el diámetro equivale a 2 radios, se establece la siguiente fórmula:
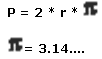
Analicemos el ejemplo:
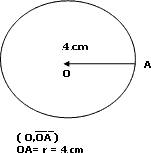
Aplicamos la fórmula:
P = 2 x 4 3,14
P = 25,12 cm.
Si calculamos 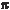 expresándolo tenemos:
expresándolo tenemos: