Triángulos y cuadriláteros

Todos los ángulos

En este número, profundizaremos el conocimiento de algunos polígonos como los triángulos y cuadriláteros. Para identificar algunas características de sus ángulos, empezaremos conociendo los ángulos que se forman con 2 rectas paralelas y una recta secante.

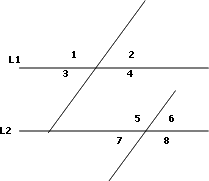
Observa con atención:

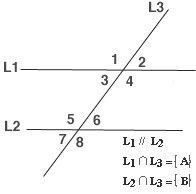
Se han formado 8 ángulos -usaremos < como símbolo de ángulo-, que tienen relación con sus medidas. Hay ángulos congruentes y ángulos suplementarios.

Angulos congruentes

Nos guiaremos por nuestro ejemplo. Primero, revisaremos los ángulos congruentes. Es decir, los que miden lo mismo. Tenemos varios casos.

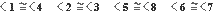
Cada par de ángulos es congruente, porque son opuestos por el vértice.

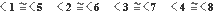
A estos ángulos, se les llama correspondientes , porque están en la misma ubicación con respecto a cada paralela, y al mismo lado de la secante.
En nuestro ejemplo, el < 1 está arriba de L1 y a la izquierda de L3. El < 5 está arriba de la otra paralela, y también a la izquierda de la secante.

Se puede comprobar que son congruentes, si hacemos un corte a la secante y superponemos los ángulos así:

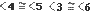
Estos ángulos son alternos internos entre paralelas. ¿Por qué son congruentes? Si el 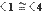 por ser opuestos por el vértice y 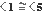por ser correspondientes, quiere decir que el .

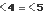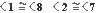
Son alternos externos.

Angulos suplementarios

A continuación, revisaremos los ángulos suplementarios , es decir los que suman 180°

– Todos los ángulos adyacentes, es decir, los que tienen un lado común son suplementarios. En nuestro ejemplo, tenemos que:

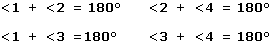
Lo mismo pasa con los otros 4 ángulos

Son interiores del mismo lado . Van dentro de las paralelas y al mismo lado de la secante.

Son exteriores del mismo lado. Van fuera de las paralelas y al mismo lado de la secante.

Se llaman contrarios o conjugados , porque van en distinta posición de las paralelas y a distinto lado de la secante.