Socios inseparables

Existen relaciones entre el plano, los puntos y las rectas que pueden llegar a producir interesantes resultados, cuyo análisis nos permite explicarnos varios aspectos de la realidad.

Plano con puntos y rectas

Estudiemos tres casos:

a) ¿Sabes cuál es la mesa que nunca queda coja? La que tiene tres patas, porque con «tres puntos del espacio se puede determinar un plano».

b) ¿Qué pasa con el plano y el espacio? El plano queda como frontera de dos semiespacios.

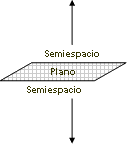
c) ¿Qué determina una recta en un plano? Forma dos subconjuntos llamados semiplanos.

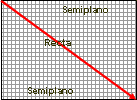
Dos rectas

En este caso, comparemos lo que sucede en el espacio y en el plano. Analicemos distintas situaciones.

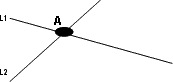
a) Si tienen un punto común. Quiere decir que su intersección, tanto en el plano como en el espacio, es un punto. A estas rectas se las llama «secantes»:

L1 n L2= {A}

Hay un caso especial de estas rectas cuando, al intersectarse, forman ángulos rectos. Aquí nos encontramos con rectas secantes perpendiculares.

Observa este ejemplo:

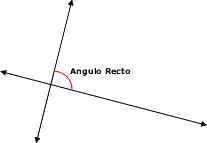
El símbolo de perpendicular es 1.En nuestro ejemplo:

L1 n L2= {P} y L1 L2

Esto lo puedes apreciar en lo que sucede con las líneas verticales y horizontales de una hoja cuadriculada.

b) Si dos rectas no cuentan con puntos comunes y tienen la misma dirección, ya sea en el espacio o en el plano, estamos hablando de rectas paralelas. Símbolo II

Por ejemplo:

En este dibujo: L1 II L2.

En la vida cotidiana, puedes apreciar este principio geométrico en el tendido de los cables que llevan electricidad, las líneas del cuaderno de composición, etcétera.

c) Rectas sin puntos comunes. También se da el caso de rectas que se cruzan, perosolamente en el espacio. No se pueden dibujar, pero sí imaginar. Pensemos en una recta que va de norte a sur cerca del techo y otra que está cerca del suelo, pero con sentido este a oeste; esas rectas se cruzan.

Estas tres relaciones que se dan entre dos rectas ocurren también entre dos planos, dos rayos, dos semirrectas o dos trazos, y entre la mezcla de estos elementos; por ejemplo, un plano y un rayo, un rayo y una semirrecta, etcétera. Sólo cambian algunos detalles.

Si dos planos son secantes, es decir que tienen intersección, esa intersección no es un punto, es una recta. Observa con atención:

Una recta es secante al plano en un punto

Todas estas ideas geométricas y sus relaciones son la base que ha utilizado el hombre para desarrollar la ciencia y la tecnología. Él ha construido sus viviendas, monumentos y obras de arte, teniendo presente estos conceptos.