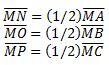Puntos notables del triángulos

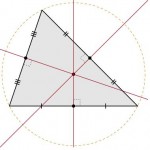Mediatrices de un triángulo

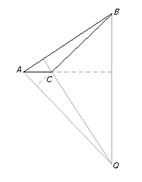
Es una recta perpendicular al lado en su punto medio. Las mediatrices de un triángulo concurren en un punto llamado circucentro, que equidista de los vértices del mismo y es centro de una circunferencia circunscrita a él.

O equidista de A
O equidista de B
O equidista de C

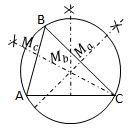
Bisectriz de un triángulo

Es la semirrecta interior del ángulo que lo divide en dos ángulos iguales. Las bisectrices de los ángulos interiores de un triángulo concurren en un punto llamado incentro, que equidista de los lados del mismo y es centro de una circunferencia inscrita a él.

Alturas de un triángulo

Se llama base de un triángulo a cualquiera de sus lados. El segmento perpendicular desde un vértice a la base opuesta o a su prolongación se llama altura. Un triángulo tiene, pues, tres bases a,b,c, y las tres alturas correspondientes, ha, hb y hc.

En un triángulo rectángulo el cuadrado de la altura sobre la hipotenusa es igual al producto de los dos segmentos en que la divide: h^2 = m ∙ n

Esta relación se conoce como teorema de la altura. Las tres alturas de un triángulo (o sus prolongaciones) se cortan en un punto llamado ortocentro. Si el triángulo es acutángulo, el ortocentro es interior al triángulo.

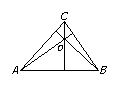
En un triángulo rectángulo, cada cateto puede ser considerado como base y como altura. El ortocentro es, por tanto, el vértice del ángulo recto. Si el triángulo es obtusángulo el ortocentro se obtiene, prolongando las alturas, fuera del triángulo.

Medianas de un triángulo

Se llama mediana de un triángulo a cada uno de los tres segmentos que unen un vértice con el punto medio del lado opuesto. Las tres medianas de un triángulo se cortan en un punto que se llama baricentro.

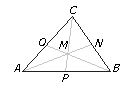
El baricentro corta a cada mediana en dos segmentos, uno de ellos la mitad del otro: