Propiedades de la inclusión y de la igualdad

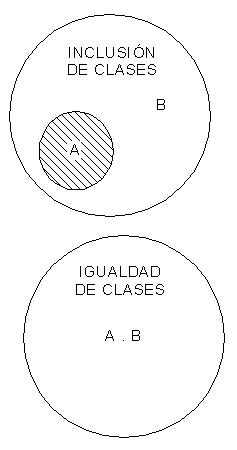Inclusión

Sean A y B dos conjuntos, si cada elemento de A es elemento de B diremos que A está incluido en B, o bien que A es parte de B, o que A es un subconjunto de B, y lo escribimos A » B.

A menudo será necesario demostrar que un conjunto es parte de otro entonces, de acuerdo a la definición, será suficiente demostrar que cualquier elemento del primero pertenece al segundo.

Asimismo, teniendo en cuenta la equivalencia entre una implicación y la contrarecíproca, la definición anterior puede expresarse así:

A » B ! » x : x » B ! x » A

Igualdad de conjuntos

Nos resulta sencillo darnos cuenta que dos conjuntos son iguales si tienen los mismos elementos. Volviendo al ejemplo anterior, supongamos ahora que todos los libros de mi colección son de matemática, entonces, que A » B, pero a su vez B » A y llegamos a la conclusión de que ambos conjuntos son iguales.

En símbolos:

A = B ! A » B » B » A

Subconjunto. Inclusión, si un conjunto S está incluido en C si y sólo si todo elemento de S pertenece a C.

Ejemplo:

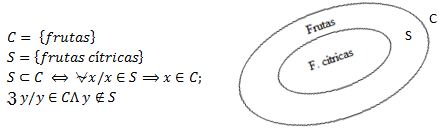
Se lee: S es subconjunto de C o S está incluido en C si, para todo x tal que x pertenece al conjunto C; pero existe algún elemento y tal que y pertenece al conjunto C y no pertenece al subconjunto S

S={lima,limón…naranja}
C={pera,banana,limón,naranja…}(definidos por extensión)

Conjuntos iguales, se dice que un conjunto M es igual al conjunto N, cuando tiene los mismos elementos que éste y todo elemento M pertenece al conjunto N y todo elemento N pertenece al conjunto M.

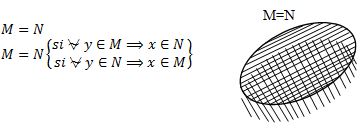
También se define la igualdad entre conjuntos por medio de la inclusión.

Dos conjuntos M y N son iguales si y sólo si el primero está incluido en el segundo y recíprocamente.

Propiedades de la inclusión de la igualdad